1) D.E.S., le chiffrement à clé secrète

a) Histoire de DES :

Au début des années 70, le N.B.S. (National Bureau of Standards) a lancé un appel dans le Federal Register pour la création d’un algorithme de cryptage répondant aux critères suivants:

un haut niveau de sécurité lié à une clé
compréhensible
ne devant pas dépendre de la confidentialité de l’algorithme
adaptable et économique
efficace et exportable

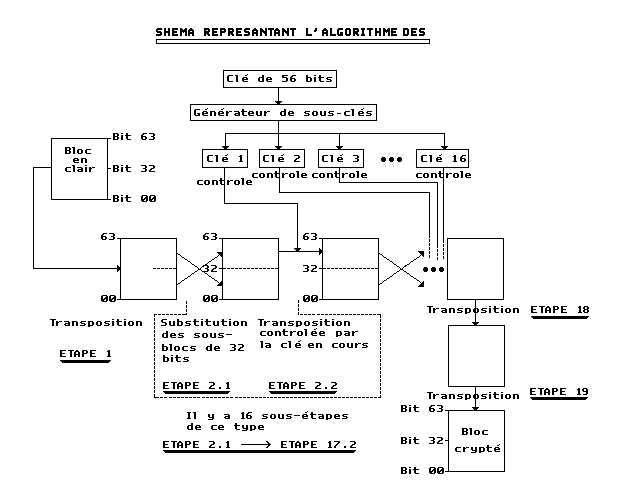
Fin 1974, IBM propose Lucifer, qui grâce à la NSA (National Security Agency) est modifié pour donner le D.E.S. (Data Encryption Standard : »standard de cryptage de données ») le 23 novembre 1976.   Le DES a finalement été approuvé en 1978 par le NBS. Le D.E.S. sert à la cryptographie et l’authentification de données. Il a été jugé si difficile à percer par le gouvernement des Etats-Unis qu’il a été adopté par le Ministère de la Défense des Etats-Unis, qui a contrôlé depuis lors son exportation. D.E.S. a été pensé par les chercheurs d’IBM pour satisfaire la demande des banques.  Il a été conçu pour être implanté directement en machine.  En effet puisque les étapes de l’algorithme étaient simples, mais nombreuses, il était possible à IBM de créer des processeurs dédiés, capables de crypter et de décrypter rapidement des données avec l’algorithme D.E.S.. Cet algorithme a donc été étudié intensivement depuis les 15 dernières années et est devenu l’algorithme le mieux connu et le plus utilisé dans le monde à ce jour. Il est réactualisé tous les 5 ans.

Bien que D.E.S. soit très sûr, certaines entreprises préfèrent utiliser le « triple-D.E.S. ». Le triple-D.E.S. n’est rien d’autre que l’algorithme D.E.S. appliqué trois fois, avec trois clés privées différentes.

b) Principes :

C’est un système de chiffrement par blocs de 64 bits uniquement, dont le dernier octet sert de test de parité (pour vérifier l’intégrité des données). Il consiste à faire des combinaisons, des substitutions et des permutations entre le texte à chiffrer et la clé, en faisant en sorte que les opérations puissent se faire dans les deux sens (pour le décryptage). La clé est codée sur 64 bits et formée de 16 blocs de 4 bits, généralement notés k₀ à k₁₅. Etant donné que 8 bits de la clé sont réservés pour le test de la parité, « seulement » 56 bits servent réellement à chiffrer, ce qui représente tout de même 2⁵⁶ possibilités, c’est-à-dire environ 72*10¹⁵ clés possibles...

Les grandes lignes de l’algorithme sont les suivantes:
DES utilise une clé secrète de 56 bits, qu’il transforme en 16 « sous-clés » de 48 bits chacune. Le cryptage se déroule sur 19 étapes.
La première étape est une transposition fixe (standard) des 64 bits à crypter.
Les 16 étapes suivantes peuvent être divisées en 2 « sous-étapes » chacune. Dans un premier temps, le bloc de 64 bits est découpé en 2x32 bits, et une substitution est effectuée entre ces deux blocs. En fait, ces deux blocs seront tout simplement échangés l’un avec l’autre. Dans un second temps, le bloc de 32 bits ayant le poids le plus fort (le bloc qui va du bit n°32 au bit n°63) subira une transposition contrôlée par la sous-clé correspondant à l’étape en cours.

Les étapes 18 et 19  sont deux transpositions.

c) Le décryptage avec l’algorithme D.E.S.

Pour décrypter un document auparavant crypté avec D.E.S., il suffit d’effectuer l’algorithme à l’envers avec la bonne clé. En effet, il n’est pas nécessaire d’utiliser un algorithme différent ou une clé différente puisque D.E.S. est comme nous l’avons vu un algorithme symétrique. Il est donc totalement et facilement réversible, si l’on possède la clé secrète.

Problèmes de la méthode

En 1990 Eli Biham et Adi Shamir ont mis au point la cryptanalyse différentielle qui recherche des paires de texte en clair et des paires de texte chiffrées (cette méthode marche jusqu’à un nombre de rondes inférieur à 15 d’où un nombre de 16 rondes dans l’algorithme présenté ci-dessus).

D’autre part, même si une clé de 56 bits donne un nombre énorme de possibilités, des processeurs permettent de calculer plus de 10⁶ clés par seconde. Ainsi, s' ils sont utilisés parallèlement sur un très grand nombre de machines, il peut être possible à un grand organisme (un Etat par exemple) de trouver la bonne clé.

2) Les modes opérationnels utilisés avec D.E.S.

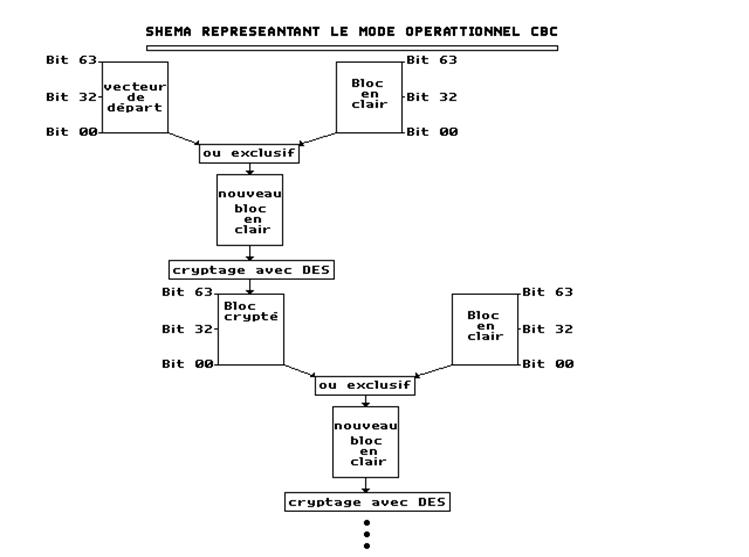
Comme nous l’avons vu, l’algorithme D.E.S. ne permet que de crypter des blocs de 64 bits. Pour crypter ou décrypter un document complet, il faut donc utiliser D.E.S. en série dans un « mode opérationnel ». Il existe beaucoup de modes opérationnels, nous n’allons voir que le mode ECB et le mode CBC.

a) Le mode opérationnel E.C.B.

ECB signifie Electronic Code Book (« catalogue électronique de codes »). Dans ce mode, on découpe le document à crypter ou à décrypter en blocs de 64 bits qu’on crypte les uns indépendamment des autres. Puisque, à chaque bloc en clair correspond un bloc crypté, pour une clé donnée, cela peut faire penser à un « catalogue de codes ».

b) Le mode opérationnel C.B.C.

CBC signifie Chain Block Cipher (« Cryptogramme à blocs chaînés »). Comme nous l’avons vu précédemment, le mode opérationnel ECB ne protège pas contre la présence de blocs redondants, puisqu’ils sont cryptés indépendamment les uns des autres. La seconde faiblesse est qu’un bloc en clair, hors contexte, et codé toujours avec la même clé, produira toujours le même bloc crypté.

Le CBC lui, répond à ces deux problèmes. Pour ce faire, avant de crypter un bloc en clair, on va effectuer un « ou-exclusif » entre ce bloc en clair et le bloc précédemment crypté. Cela nous donnera un nouveau bloc en clair que l’on cryptera.

En plus de posséder une clé secrète en commun, les deux interlocuteurs doivent dorénavant se mettre d’accord sur un bloc de 64 bits de départ qu’on appellera « vecteur de départ », ou « vecteur initial ».

3) Procédé PKC (Public Key Cryptosystem).

Bien que moins performant que le DES, il élimine cependant le problème de distribution des clés en utilisant à la fois une clé de chiffrage publique, transmise sans cryptage, et une clé de déchiffrage privée qui n’est accessible qu’au destinataire du message. Il est ainsi possible d’assurer la confidentialité de la transmission tout en authentifiant l’émetteur du message. Il s’agit donc d’une signature électronique, permettant par exemple la réalisation de transactions commerciales sur un réseau public, notamment sur Internet. La plupart des PKC sont fondés sur les propriétés mathématiques des nombres premiers. Les systèmes de cartes bancaires à puce, qui authentifient leur possesseur par un code secret, sont fondés sur les mêmes principes.